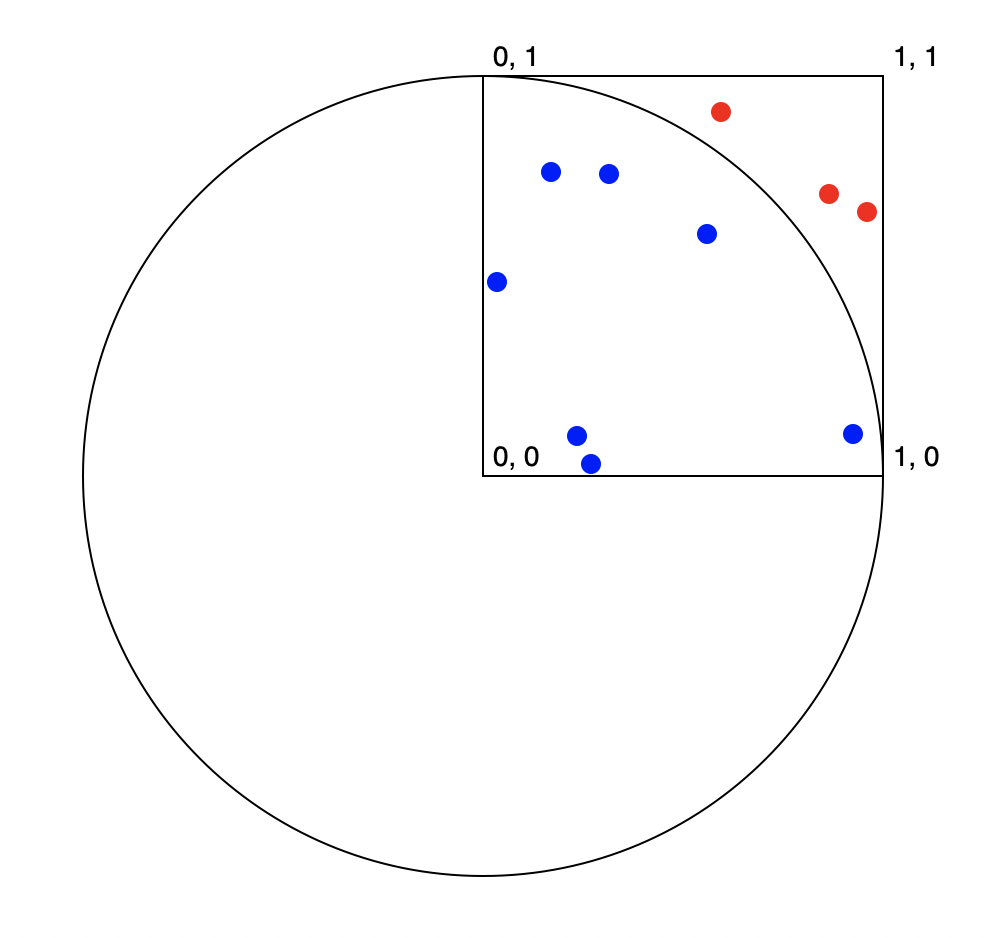
L'exemple traditionnel des méthodes de Monte-Carlo est le calcul de \(\pi\).
L'idée est simple. De manière répétée, on place des points uniformément au hasard dans un carré de dimension 1 par 1. On compte combien de ces points sont tombés dans un cercle de rayon 1 qui a pour centre un des coins du carré. La fraction des points qui tombent dans le cercle permet de calculer une estimation de \(\pi\).

En effet, l'intersection entre le cercle et le carré a une surface de \(\frac{\pi \cdot r^2}{4}\), avec \(r = 1\). Le carré quant à lui a une surface de \(1\). La proportion de points qui tombent dans le cercle devrait donc se reprocher de \(\frac{\pi}{4}\). Une fois cette proportion estimée par une simulation de Monte-Carlo, il est simple d'obtenir une estimation de \(\pi\).
Concevez un script pour estimer la valeur de \(\pi\) grâce à la technique décrite plus haut. Essayez de changer le nombre d'itérations et observez l'influence sur le résultat obtenu.
Pour calculer un point aléatoire, une suffit de tirer aléatoirement une valeur pour l'abscisse et une autre valeur pour l'ordonnée.
La méthode random du module random permet de retourner une valeur aléatoire dans l'intervalle \([0, 1[\).
Pour savoir si un point tombe dans le cercle, il suffit de calculer la distance euclidienne entre le point et le centre du cercle. Si cette distance est inférieure ou égale au rayon du cercle, alors le point est à l'intérieur du cercle.
Pour rappel, la distance euclidienne entre deux points \((x_1, y_1)\) et \((x_2, y_2)\) est donné par la formule \(\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\).
Dans le cas présent, comme un des points est à l'origine, la formule se simplifie grandement.
Pour cet exercice, nous allons aborder le jeu du Blackjack.
Le Blackjack est un jeu d'argent utilisant des cartes où un ou plusieurs joueurs affrontent un croupier. Le jeu est relativement simple. Pour participer au jeu, chaque joueur met en jeu un montant appelé une mise. Le croupier distribue une carte à chaque joueur, puis à lui-même. Le croupier dévoile sa première carte aux joueurs. Le croupier distribue ensuite une deuxième carte à chaque joueur et à lui-même. Le croupier ne dévoile pas sa seconde carte. Les cartes d'un joueur constituent sa main.
Chaque carte a une valeur qui est donnée par le tableau suivant :
| Carte | Valeur |
|---|---|
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | 10 |
| Valet | 10 |
| Dame | 10 |
| Roi | 10 |
| As | 1 ou 11 (au choix) |
Ainsi, chaque main a une valeur qui est la somme des cartes qui la composent. Si une main contient un ou plusieurs As, le joueur à qui le jeu appartient décide de la valeur de chaque As indépendamment. Un As peut ainsi soit valoir 1, soit valoir 11.
Le but est d'avoir un meilleur jeu que celui du croupier sans toutefois dépasser la valeur de 21 points. À leur tour, chaque joueur peut demander des cartes au croupier afin d'augmenter la valeur de son jeu, en espérant toutefois ne pas dépasser les 21 points, auquel cas le joueur serait d'office éliminé et perdrait sa mise.
Un cas particulier se présente lorsque le joueur (ou le croupier) a une main initiale de deux cartes qui totalise directement 21 points, ce qui est possible avec un As et une carte entre le 10 et le Roi. On appelle cette main un Blackjack.
À son tour de jouer, chaque joueur peut :
Une fois que chaque joueur a effectué ses actions, c'est au croupier de jouer. Il révèle sa carte cachée aux joueurs. Finalement, le croupier tire des cartes selon une stratégie bien définie. Tant que la valeur du jeu du croupier est en dessous ou égal à 16, il prend une carte supplémentaire. Dès que 17 points ou plus sont obtenus, le croupier s'arrête.
Une fois que le croupier a joué, arrive la détermination des gains. Les gains sont déterminés selon les étapes suivantes, à suivre dans l'ordre :
Chaque joueur qui a dépassé les 21 points perd immédiatement sa mise et quitte le jeu.
Si le croupier a un Blackjack (21 points sur les deux premières cartes), alors tous les joueurs perdent immédiatement leur mise, sauf s'ils ont aussi un Blackjack. Si un joueur a un Blackjack en même temps que le croupier, alors il y a égalité entre eux et le joueur récupère simplement sa mise. Dans tous les cas tous les joueurs quittent ensuite le jeu.
Un joueur qui a eu un Blackjack (21 points sur les deux premières cartes) récupère sa mise et gagne en plus 1.5 fois sa mise, sauf si le croupier a eu un Blackjack comme discuté plus haut. Le joueur quitte ensuite le jeu.
Si le croupier dépasse les 21 points, alors tous les joueurs encore en jeu récupèrent leur mise puis gagnent une fois leur mise et quittent le jeu.
Si un joueur a un meilleur score que le croupier, il récupère sa mise et en plus gagne une fois sa mise. Il quitte ensuite le jeu.
Si un joueur a exactement le même score que le croupier, il récupère simplement sa mise et quitte le jeu.
Finalement, chaque joueur qui a obtenu un plus petit score que le croupier perd sa mise et quitte le jeu.
Dans cet exercice, vous allez compléter un code existant pour implémenter un simulateur pour le Blackjack. Ce simulateur vous permettra d'estimer quel est le meilleur coup à jouer étant donné une main et une carte visible pour le croupier. Il vous permettra aussi d'estimer l'espérance de gain au Blackjack et de déterminer quelles sont les meilleures mains de départ.
Un ensemble de fichiers vous est fourni pour cet exercice. Vous pouvez télécharger l'archive ci-dessous.
Télécharger les fichiers de l'exercice.
Vous pouvez placer les fichiers dans un dossier blackjack dans votre espace de stockage.
En première partie d'exercice, implémentez les méthodes manquantes de la classe Hand située dans le fichier state.py.
Les méthodes manquantes sont décrites ci-dessous.
get_non_bust_hand_valuesLa méthode get_non_bust_hand_values doit retourner la liste des valeurs possibles pour la main qui ne dépassent pas 21 points.
Évitez les duplicats.
Indice : Quand une main n'a pas d'As, la situation est relativement simple car il n'y a qu'une seule valeur possible.
Indice : Quand une main a un ou plusieurs as, au maximum un seul de ces As pourra prendre une valeur de 11.
get_best_hand_valueLa méthode get_best_hand_value doit retourner la plus haute valeur possible pour la main qui ne dépasse pas 21 points, ou None si cela n'est pas possible.
is_bustLa méthode is_bust doit indiquer si la main dépasse de toutes manières les 21 points.
is_blackjackLa méthode is_blackjack doit indiquer si la main est un Blackjack, c'est-à-dire si elle contient 2 cartes et peut arriver à 21 points.
Essayez le script main.py.
Comparez les résultats obtenus à ceux présentés dans l'article Wikipédia sur le Blackjack.
Dans un nouveau fichier stats.py, faites en sorte d'estimer le gain moyen d'une partie de Blackjack.
Si cet exercice vous intéresse, il y a de noubreuses pistes à explorer pour explorer plus en profondeur le jeu du Blackjack. Ci-dessous sont listées quelques idées d'approfondissement.