serie1

Dans cet exercice, nous allons nous intéresser à la résolution d'un jeu de stratégie de la famille des jeux de Nim.

Dans le jeu que nous allons considérer, deux joueurs s'affrontent autour de \(n\) allumettes. Chacun leur tour, chaque joueur doit retirer 1, 2 ou 3 allumettes. Le joueur qui arrive à retirer la dernière allumette est déclaré gagnant.

Pour cet exercice, nous allons essayer de déterminer la façon optimale de jouer à ce jeu à l'aide d'un programme Python.

Pour cela, nous allons concevoir une fonction appelée winning_move. La fonction a un unique paramètre n qui représente le nombre d'allumettes encore en jeu.

def winning_move(n):
    pass

Implémenter cette fonction n'est à priori pas trivial. Dans un premier temps, nous allons concevoir cette fonction de manière récursive. La récursion est un outil de résolution de problème très puissant qui nous permettra de facilement obtenir une implémentation. Une fois cette fonction implémentée, nous pourrons étudier ses résultats et mettre au point une fonction plus directe.

Cas de base

Dans toute fonction récursive, il y a ce qu'on appelle un cas de base. Pour le cas de base, la solution est obtenue de façon immédiate, sans avoir à effectuer un appel récursif. Dans le cas présent, le cas de base survient quand il reste en jeu de 1 à 3 allumettes. En effet, dans le cas où il reste entre 1 et 3 allumettes, la stratégie gagnante consiste de manière assez évidente à enlever le reste des allumettes.

Faites donc en sorte que votre fonction winning_move retourne bien le bon nombre d'allumettes à retirer dans le cas où il y a trois allumettes ou moins en jeu.

Cas récursif

Dans certains cas, comme par exemple pour 4 allumettes, il n'y a pas de coup qui amène de façon certaine à une victoire (ce que l'on appelle un coup gagnant). En effet, lorsqu'il reste 4 allumettes, peu importe le nombre d'allumettes retirées, l'adversaire aura ensuite la possibilité de jouer un coup gagnant. Quoi que l'on fasse, l'adversaire sera ensuite dans une position gagnante, une position où il sera capable d'assurer la victoire en jouant le bon coup. Si chaque coup amène à une position gagnante de l'adversaire, on est dans une position perdante. Dans le cadre de la fonction winning_move, on utilise la valeur de retour None pour représenter que la position est perdante.

Dans le cas où il y a plus de 3 allumettes en jeu, il est possible de déterminer si la position est gagnante ou perdante, et le cas échéant quel est le coup gagnant, de manière récursive grâce à aux observations suivantes.

Soit un jeu avec \(n > 3\) allumettes restantes. Si la situation avec \(n - 1\) allumettes est une situation perdante, alors jouer \(1\) allumette est un coup gagnant. En effet, on place ainsi l'adversaire dans une situation perdante, une situtation où quoi qu'il joue on se retrouvera à nouveau en position gagnante. Le raisonnement est le même pour le cas où \(n - 2\) ou \(n - 3\) allumettes sont des positions perdantes. Dans ces cas, il faudrait donc retirer 2, respectivement 3, allumettes afin d'être assuré ensuite de gagner.

Cependant, dans le cas où il existe un coup gagnant pour \(n - 1\), \(n - 2\) et \(n - 3\) allumettes, alors il n'existe pas de coup gagnant pour le joueur courant. En effet, quoi qu'il fasse, l'adversaire aura un coup gagnant à jouer. C'est ce qui se présente dans le cas où il reste 4 allumettes en jeu. En effet, peu importe que l'on retire 1, 2 ou 3 allumettes, le coup d'après l'adversaire pourra gagner. La position est donc perdante.

Implémentation directe

Une fois votre fonction implémentée, essayez d'afficher la valeur retournée par votre fonction pour tous les nombres de 1 à 20. Pouvez-vous en dériver une implémentation plus directe faisant usage d'une opération arithmétique ?

Cette version plus directe est intéressante car elle est beaucoup plus rapide que la version récursive. Elle est aussi plus facile à mettre en application de tête, sans l'usage d'un ordinateur.

Exercice 2 : Tours de Hanoï

Le jeu des tours de Hanoï est un jeu de réflexion pour un seul joueur. Dans ce jeu, une tour pyramidale formée de disques doit être déplacée d'une position 0 à une position 2, disque par disque, et ce le plus efficacement possible. Une position 1 peut être utilisée afin de stocker de façon temporaire des disques.

Dans cet exercice, nous allons concevoir une fonction pour réaliser cette tâche. La fonction aura pour nom move_tower et aura 3 paramètres :

La fonction doit retourner une liste de mouvements à effectuer. Chaque mouvement est de la forme (a, b) et indique que le disque au sommet de la pyramide en position a a été déplacé au sommet de la pyramide en position b.

Exemple

La valeur de retour attendue pour le déplacement d'une pyramide de hauteur 2 de la position 0 à la position 2 est la suivante :

[(0, 1), (0, 2), (1, 2)]

En effet, on commence par déplacer le petit disque de la position 0 à la position 1, puis on déplace le grand disque de la position 0 à la position 2. Finalement, on déplace le petit disque de la position 1 à la position 2.

Méthode de résolution

Pour résoudre cette tâche, il est intéressant de procéder de manière récursive sur la taille de la pyramide à déplacer. En effet, déplacer une tour de taille 1 (voire même 0) est trivial. Il s'agit du cas de base.

Le cas récursif est un petit peu plus compliqué. Il nous faudra faire une observation cruciale pour nous guider vers une solution : Pour déplacer une tour de taille \(n > 1\) d'une position a à une position b, il faudra forcément à un moment que tous les disques sauf le plus grand soient placés sur la position tierce c, comme dans l'image ci-dessous :

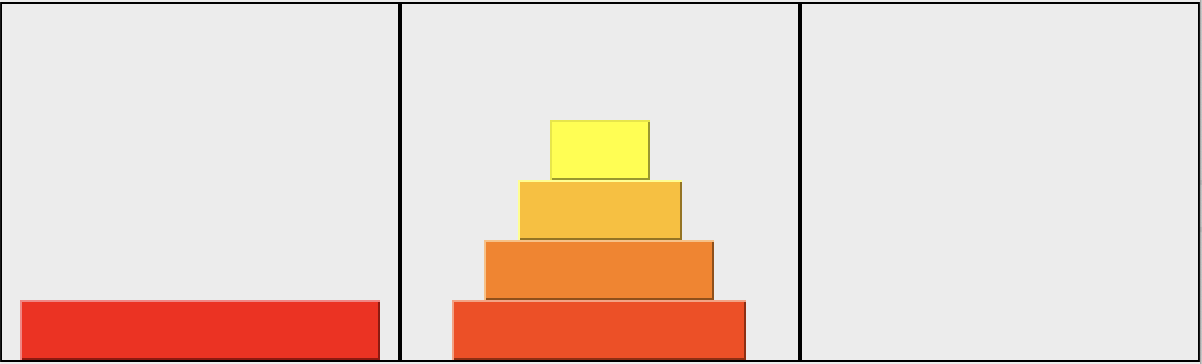
En effet, sans cela, il serait impossible de déplacer le plus grand disque, initiallement à la base de la tour, de la position a à la position b. Les disques plus petits ne peuvent pas être à la position de départ, sans quoi le grand disque ne pourrait être enlevé, ni à la position d'arrivée, sans quoi le grand disque ne pourrait y être déposé. Il y aura donc forcément tous les disques plus petits sur cette autre position, arrangée de la seule façon possible : comme une pyramide.

Une fois cette tour de taille \(n - 1\) déplacée sur la position tierce, il suffit de déplacer le plus grand des disques à sa place finale, puis de déplacer la tour de taille \(n - 1\) à nouveau, cette fois à sa place finale.

Interface graphique

Afin de vous aider à visualiser la liste des mouvements effectués et à vérifier si votre implémentation est correcte, le code d'une interface graphique vous est fournie. Vous pouvez télécharger le fichier hanoi_ui.py et le placer à côté de votre script. Ensuite, il suffit d'importer puis d'appeller la fonction start_ui comme suit :

from hanoi_ui import start_ui

n = 5
moves = move_tower(n, 0, 2)  # Appel à votre fonction

start_ui(n, moves)

Vous pourrez ensuite examiner les mouvements effectués de manière plus visuelle.

Exercice 3 : Variante d'un jeu de Nim

Dans l'exercice 1, nous avons implémenté une fonction pour déterminer le coup gagnant d'un jeu de Nim. Dans le jeu que nous avons considéré, le gagnant du jeu était celui qui arrivait à retirer la dernière allumette d'un tas de \(n\) allumettes.

Dans cet exercice, nous allons nous intéresser à une variante de ce jeu dans lequel le joueur qui retire la dernière allumette n'est pas le gagnant mais le perdant.

Comme dans l'autre variante, chaque joueur doit à son tour retirer entre 1 et 3 allumettes. Le joueur qui est forcé de retirer la dernière allumette perd la partie.

De façon similaire à l'exercice 1, concevez une fonction récursive qui vous indique, s'il existe, le nombre d'allumettes à retirer afin de gagner le jeu en fonction du nombre d'allumettes restantes. Une fois cette fonction implémentée, étudiez ses résultats et mettez au point une implémentation plus directe de la fonction.

Aller plus loin

Pour augmenter encore la difficulté du jeu, il est possible de changer le nombre d'allumettes qui peuvent être enlevées. Par exemple, à la place de pouvoir enlever 1, 2 ou 3 allumettes, on pourrait imaginer permettre uniquement d'enlever 1, 3 ou 4 allumettes, mais pas 2. Dans ce cas, les coups optimaux sont les suivants jusqu'à une taille de 20 allumettes :

 1 -> 1
 2 -> None
 3 -> 3
 4 -> 4
 5 -> 3
 6 -> 4
 7 -> None
 8 -> 1
 9 -> None
10 -> 1
11 -> 4
12 -> 3
13 -> 4
14 -> None
15 -> 1
16 -> None
17 -> 1
18 -> 4
19 -> 3
20 -> 4

Concevez une fonction qui prend en arguments une taille et une liste de coups possibles et retourne le coup à jouer, ou None si la position est perdante. Il vous faudra certainement faire appel à de la récursion. Il est probable cependant qu'une version récursive simple devienne très lente plus le nombre d'allumettes augmente.

Afin de grandement améliorer l'efficacité de votre fonction, vous pouvez faire appel à une technique qui s'appelle la programmation dynamique :

En regardant les appels récursifs de plus près, on observe que certains appels sont réalisés à de nombreuses reprises avec les mêmes arguments. À la place de recalculer ces résultats à chaque fois, on utilise une structure de donnée, comme une liste en Python, pour les stocker. À la place de faire des appels récursifs potentiellement coûteux, on consulte la liste des valeurs précalculées. Si la liste n'est pas suffisamment grande, on la remplit avec les résultats attendus.

Par exemple, voici une implémentation Python de la de la suite de Fibonacci basée sur la programmation dynamique :

fibs = [0, 1]

def fib(n):
    while len(fibs) <= n:
        fibs.append(fibs[-2] + fibs[-1])
    return fibs[n]

La liste fibs contient les valeurs de la suite de Fibonacci. À l'appel de la fonction fib, on s'assure que suffisament de valeurs de la suite ont été calculées. Si ce n'est pas le cas, on ajoute les éléments nécessaires à la liste en faisant référence aux éléments déjà présents. Ensuite, on consulte simplement la liste pour la valeur de retour de la fonction.

Série 1

Exercice 1 : Jeu de Nim